Question

Which side lengths represent the side of a right triangle

Answer 1

B) 7, 24, 25

Step-by-step explanation

The sides of a right triangle always satisfy the Pythagorean Theorem,

`c^2=a^2+b^2`

Where a and b are the legs, and c is the hypotenuse - which is the longest side.

Thus, to answer this question, we have to see for what set of lengths the sum of the squares of the shortest ones is equal to the square of the longest one.

• For 2, 3, 5,

`\begin{gathered} 5^2=2^2+3^2 \\ 25=4+9 \\ 25=13\rightarrow FALSE \end{gathered}`

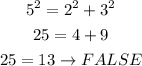
So, this set does not represent a right triangle.

• For 7, 24, 25,

`\begin{gathered} 25^2=7^2+24^2 \\ 625=49+576 \\ 625=625\rightarrow TRUE \end{gathered}`

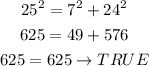
So, this set does represent a right triangle.

• For 7, 23, 25,

`\begin{gathered} 25^2=7^2+23^2 \\ 625=578\rightarrow FALSE \end{gathered}`

This set does not represent a right triangle.

• For 12, 16, 21,

`\begin{gathered} 21^2=12^2+16^2 \\ 441=400\rightarrow FALSE \end{gathered}`

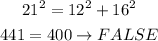
This set does not represent a right triangle.

Hence, the side lengths that represent the lengths of the sides of a right triangle are 7, 24, 25.