The speed of the ball just before it hits the ground is given by:
![v=\sqrt[]{v^2_x+v^2_y}](https://img.qammunity.org/2023/formulas/physics/college/b1061y4obi6re8od41e46k9muims0av3n1.png)
the horizontal component of the velocity is constant in the complete trajectory, then:
vx = 5 m/s
the vertical component of the velocity is calculated by using the following formula, for the speed in a free fall motion:
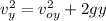
voy is the initial vertical component of the velocity and in this case is
voy = 0m/s.
g: gravitational acceleration constant = 9.8m/s^2
y: vertical distance traveled by the ball = 5 m
Solve the previous equation for vy and replace the values of the other parameters:
![\begin{gathered} v_y=\sqrt[]{2gy} \\ v_y=\sqrt[]{2(9.8(m)/(s^2))(5m)} \\ v_y\approx9.90(m)/(s) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/hfhslyfv01sabfxx6gku9lexwgtevmc0xn.png)
Then, by replacing the values of vx and vy, you obtain for v:
![\begin{gathered} v=\sqrt[]{(5(m)/(s))^2+(9.90(m)/(s))^2} \\ v\approx11.10(m)/(s) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/bklitiknltemuvqxzz3ap3favy7yfkdjvq.png)
Hence, the speed of the ball before it hits the ground is approximately 11.10m/s