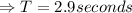Solution:
The equation is given below as
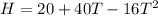
Step 1:
To determine the time when the height is at H=30, we will substitute the value of H=30 in the equation above and solve for T
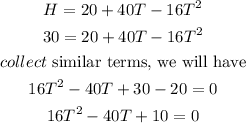
Using the quadratic formula below, we will find the value of T as

Graphically,
Hence,
The time at which the height of the helicopter will be H=30 is at
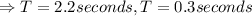
Part B:
To figure out the time at which the height will be H=0, we will substitute the value of H=0 in the equation below and solve for T
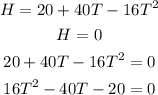
To figure out the value of T, we will use the formula below
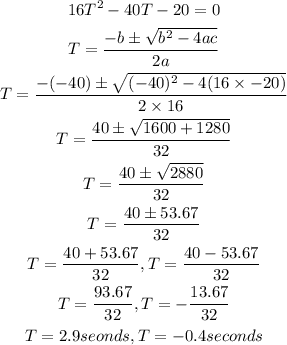
Hence,
The time at which the remote control helicopter will hit the ground at H=0 will be