Question

I need help with this question for part a and b

Answer 1

ANSWERS

a) 0%

b) 30.23%

Step-by-step explanation

The life of the streetlights, X, is normally distributed with a mean of 400 days and a standard deviation of 40 days,

`X=N(400,40)`

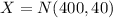
a) We have to find what percentage of lamps will last longer than 600 days. This is the same as the probability that a lamp will last more than 600 days, written as a percentage. So we have to find,

`P(X>600)`

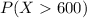
We have to standardize the variable to use the standard normal curve,

`P(X>600)=P\mleft((X-\mu)/(\sigma)>(600-\mu)/(\sigma)\mright)=P\mleft(Z>(600-400)/(40)\mright)=P(Z>5)`

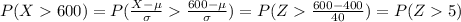
As expected, this probability is 0. So the percentage of lamps that last longer than 600 days is 0%.

Note that the mean life is 400 days, and 600 days is 200 days past that mean life. If the standard deviation is only 40 days, it is expected that no lamp could last longer than 600 days.

b) Now, we have to find the probability that a lamp lasts between 420 and 500 days. We can sketch the normal curve to understand what we are looking for,

A Z-table shows the probability that the variable is less than a value - i.e. the area under the curve to the left of the value. So, this probability is the probability that X is less than 500 minus the probability that X is less than 420,

`P(420Use the same method we used before to standardize the variable,[tex]P(Z<(500-400)/(40))-P(Z<(420-400)/(40))=P(Z<2.5)-P(Z<0.5)`

Find these two values in a Z-table,

So the probability is,

[tex]P(420Multiply by 100 to obtain the percentage.

Hence, the percentage of the lamps that last between 420 and 500 days is 30.23%.