we use a tool to graph
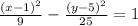
now find the value of c, c is the distance between foci and find it using
![c=\sqrt[]{a^2+b^2}](https://img.qammunity.org/2023/formulas/mathematics/college/6uwqakmkjq6nua21bpopztkrf20jt2flji.png)
where a and b are the roots of the denominator on the original function
a=3 and b=5
![\begin{gathered} c=\sqrt[]{3^2+5^2} \\ c=\sqrt[]{34} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wybgujixvxex9lj3otipeckr2cxnbc0vre.png)
the parabola is moved to right 1 unit then we need to add 1 to the measure
![c=1\pm\sqrt[]{34}](https://img.qammunity.org/2023/formulas/mathematics/college/34g9vzgt6vvj19c1gega64ixppi34adpyp.png)
we have two solutions for c because we have 2 foci
the general form of the foci points on this exercise is
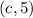
y is 5 because it is the transversal axis of the function now replace the two values of c to find the foci
![\begin{gathered} (1+\sqrt[]{34},5) \\ (1-\sqrt[]{34},5) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/w903esxog61aey785ye5d7fo9j5fjgatdy.png)
then right option is the last