Answer:
10th term = 90
Explanations:
-9, 2, 13, 24, ....................
This is an Arithmetic Progression because it has a common difference
Let the common difference be represented as d
d = 2 - (-9)
d = 2 + 9
d = 11
The nth term of an Arithmetic Progression is given by the equation
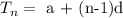
where a is the first term
n is the number of terms
d is the common difference
To find the 10th term, substitute n=10, d = 11, and a = -9 into the equation for nth term given above
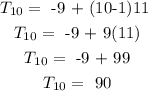
The 10th term of the sequence is 90