Question

_______ 10. Given the following information, find the length of chord AC.OA = 5. OB = 3A. 4B. 5C. 6D. 8

Answer 1

Hello there. To solve this question, we'll have to remember some properties about the radius of a circle and the Pythagorean Theorem.

Given the following diagram:

We want to determine the length of the chord AC.

We already know that the length of the segments OA = 5 and OB = 3.

In the diagram, we get

Notice this is a right triangle, therefore we can determine the length of the segment AB by using the Pythagorean Theorem.

We know that

`\overline{AB}^2+\overline{OB}^2=\overline{OA}^2`

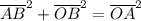
Hence we get that

`\begin{gathered} \overline{AB}^2+3^2=5^2 \\ \\ \overline{AB}^2+9=25 \\ \\ \overline{AB}^2=25-9=16 \\ \\ \overline{AB}=√(16)=4 \\ \end{gathered}`

Since OA is the radius of the circle and D is the midpoint of the arc AC, we get that

`\overline{OA}\equiv\overline{OC}`

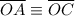
Which means that

`\overline{AB}\equiv\overline{BC}`

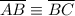
Since

`\overline{AC}=\overline{AB}+\overline{BC}`

We get that

`\overline{AC}=4+4=8`

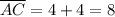
This is the final answer and contained in the last option, D. 8;