Given the system of equations, notice that we can divide by -2 the second equation to get the following equivalent equation:
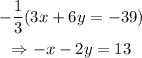
then, we woul have the following equivalent system of equations:
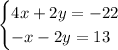
if we add both equations, we can find the value of x:
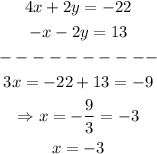
now that we know that x = -3, we can use this value to find the value of y:
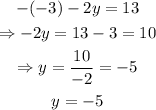
therefore, the solutions are x = -3 and y = -5