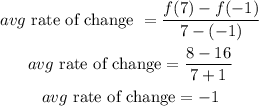Question

Given the function f(x) = x^2 - 7x + 8 determine the average rate of change of the function over the interval -1 ≤ x ≤ 7

Answer 1

-1

Explanation

The average rate of change of function f(x) over the interval a ≤ x ≤ b is calculated as follows:

`avg\text{ rate of change }=(f(b)-f(a))/(b-a)`

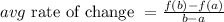
where f(b) and f(a) are the function f(x) evaluated at x = b and x = a respectively.

In this case, the function is:

`f(x)=x^2-7x+8`

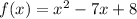
And the interval is -1 ≤ x ≤ 7. Evaluating f(x) at x = 7 and x = -1:

`\begin{gathered} f(7)=7^2-7\cdot7+8 \\ f(7)=49-49+8 \\ f(7)=8 \\ f(-1)=(-1)^2-7\cdot(-1)+8 \\ f(-1)=1+7+8 \\ f(-1)=16 \end{gathered}`

Then, the average rate of change of this function is:

`\begin{gathered} avg\text{ rate of change }=(f(7)-f(-1))/(7-(-1)) \\ avg\text{ rate of change}=(8-16)/(7+1) \\ avg\text{ rate of change}=-1 \end{gathered}`