649896937097746763718057807743677852659253658762654364666450Indicate the number of bins for your histogram: ________What size should your intervals be? Show your calculations: _…

Question

asked May 7, 2023 59.0k views

1 Answer

Martin Schimak · Answer 1 · 2023-05-12T03:44:05+0000

Hello there. To solve this question, we have to remember some properties about histograms.

Given the following data, we want to determine:

649896

937097

746763

718057

807743

677852

659253

658762

654364

666450

a) The number of bins in the histogram

For this, we use the following formula:

$\text{bins}=1+\lceil\log_2(n)\rceil$

In this case, we have 30 values, hence

$\text{b}\imaginaryI\text{ns}=1+\operatorname{\lceil}\operatorname{\log}_2(30)\operatorname{\rceil}\approx1+5=6$

b) What size should your intervals be?

For this, we want to determine the width of a bin.

Using the following formula:

$\text{ bin width }=(\max(x)-\min(x))/(bins)$

Where max(x) represents the maximum value in the data set, min(x) is the minimum value and bins is the number we found on a).

We get that max(x) = 98 and min(x) = 43, hence

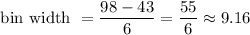
$\text{ bin width }=(98-43)/(6)=(55)/(6)\approx9.16$

These are the answers to this question.