Given the system of equations,
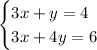
To use the elimination method, the better option is to eliminate the x variable, since the coefficient that accompanies x in both equations is the same. Then, subtracting the first equation from the second one,
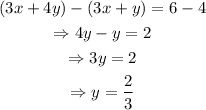
Then, we can use the value of y to find x, as shown below
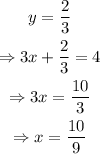
The better option is to eliminate x first because its coefficient is the same (3) in both equations.