Step1: Pick 2 points in the table:
(0,6) and (4,10)
Step2: Recall the formula for the slope of a line.
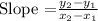
Step3: Substitute the values of the coordinates in the above formula.
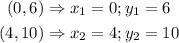
Step4:
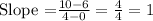
Step5: Invoke the formula for the equation of the line.
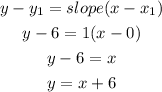
Hence, the correct answer is y = x + 6