Question

If the angle of elevation of the sun is 61.7° when a building casts a shadow of 56.5 feet, what is the height of the building rounded to the nearest tenth of a foot?

Answer 1

Let us use a simple diagram to interprete the question

In the diagram above, the dark stuff below represents the shadow and the rectangular bar represents the building. I have labelled the height of the building as h.

So we will use the right-angled triangle formed to find h

As we can see h represents the opposite side and 56.5 feet represents the adjacent side of the right-angle triangle. So we will use TOA

`\text{TOA tan }\theta=\frac{opposite}{\text{adjacent}}`

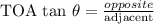
So we have

`\begin{gathered} \text{ tan }\theta=\frac{opposite}{\text{adjacent}} \\ \text{ tan }61.7\degree=(h)/(56.5) \\ 1.8572015=(h)/(56.5) \\ \text{cross multiplying, we have } \\ h=1.8572015*56.5 \\ h=104.931887 \end{gathered}`

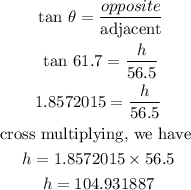
Hence the answer is 104.9 feet to the nearest tenth