A diagram of the given problem is the following:
To determine the distance "x" from the interface between the water and the oil of the block we need to add the forces that are acting on the system. We have the following:
Where:

Since the system is in equilibrium this means that the total sum of forces adds up to zero:
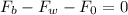
Now, the force is the product of the pressure by the area, therefore, we have:
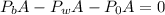
We can cancel out the area:
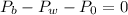
The pressure is the hydrostatic pressure and is given by:
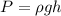
Where:

Substituting in the equation we get:
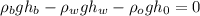
Now, we substitute the values of the heights according to the first diagram:
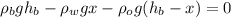
Now, we solve for "x". To do that we will apply the distributive property on the parenthesis:
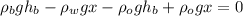
Now we associate terms according to the value of the height:
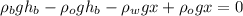
Now, we take common factors:
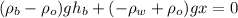
We can cancel out the gravity:
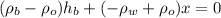
Now, we bring the terms with the height of the block to the right side:
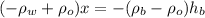
Now, we divide both sides by the factor of "x":
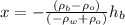
Now, we plug in the values:
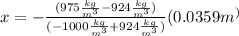
We converted the height of the block using the following conversion factor:
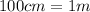
Now, we solve the operations, we get:
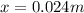
Therefore, the distance between the interface and the bottom of the block is 0.024 meters.