We have a direct variation between x and y.
We can write this as:
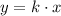
where k is a constant.
Knowing one point of the relation, like (-2,-8) we can calculate k as:
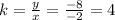
Then, if we have the point (x,36), we have to calculate the value of x.
As we know that y = 36 and k = 4, we can find x as:
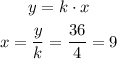
Answer: the missing value is x = 9