1 Answer

Ask a Question

Venkat Peri · Answer 1 · 2023-10-18T13:31:35+0000

We know that

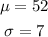
$\begin{gathered} \mu=52 \\ \sigma=7 \end{gathered}$

If X is a normally distributed random variable with mean 52 and standard desviation 7, the probability that X is between 45 and 59 is represented as

$P(45Then, we must write 45 and 59 as the mean 52 plus or minus a multiple k of the standard desviation 7[tex]\begin{gathered} 45=\mu+\sigma k \\ 45=52+7k \\ 7k=45-52 \\ k=-1 \end{gathered}$

So,

$45=\mu-\sigma$

By a similar calculation

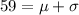
$59=\mu+\sigma$

This means

[tex]P(45taking into account that X is normally distributed and using the 0.68-0.95-0.997 rule[tex]P(\mu-\sigmaSo, P (45 < X < 59) = 0.68

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions