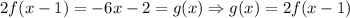Question

Use the graphs of f and g below to selection the function that matches g

Answer 1

To answer this question, we have that both functions are linear functions defined in some intervals. We can find the line equations for those lines as follows:

Finding function f in the interval [-2, -1]

1. We need to define the function f using the points:

(-2, 2) and (-1, -1).

Using these points, we can find the line equation using the two-point form of the line equation:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

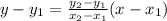
(-2, 2) ---> x1 = -2, y1 = 2

(-1, -1) ---> x2 = -1, y2 = -1

`y-2=(-1-2)/(-1-(-2))(x-(-2))\Rightarrow y-2=(-3)/(-1+2)(x+2)`
`y-2=(-3)/(1)(x+2)\Rightarrow y-2=-3(x+2)=-3x-6_{}`
`y-2=-3x-6\Rightarrow y=-3x-6+2\Rightarrow y=-3x-4`
`f(x)=-3x-4`

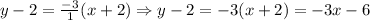
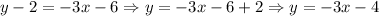
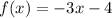
Therefore, the function f(x) = -3x - 4 in the interval [-2, -1]

Finding the function g in the interval [-1, 0]

To find the function g, we can proceed in a similar way:

1. We have the following points:

(-1, 4) and (0, -2)

Then, we have:

(-1, 4) ---> x1 = -1, y1 = 4

(0, -2) ---> x2 = 0, y2 = -2

2. Applying the two-point form of the line, we have:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)\Rightarrow y-4=(-2-4)/(0-(-1))(x-(-1))`
`y-4=(-6)/(1)(x+1)\Rightarrow y-4=-6x-6`
`y=-6x-6+4\Rightarrow y=-6x-2\Rightarrow g(x)=-6x-2`

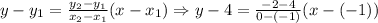
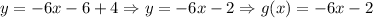
Therefore, the function g(x) = -6x - 2 in the interval [-1, 0].

If we use the given options in the question, we have that:

`g(x)=2f(x-1)`

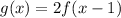
We have that:

`2f(x-1)\Rightarrow f(x-1)\Rightarrow f(x-1)=-3(x-1)-4_{}`

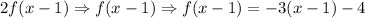
Then, we have:

`f(x-1)=-3x+3-4=-3x-1`

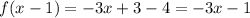
Then

`2f(x-1)=2(-3x-1)=-6x-2`

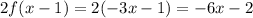
Therefore

`2f(x-1)=-6x-2=g(x)\Rightarrow g(x)=2f(x-1)`