1 Answer

Lecko · Answer 1 · 2023-07-20T10:18:16+0000

You can identify that the triangle is a Right Triangle because it has an angle that measures 90 degrees.

Then, you can use the following Trigonometric Function:

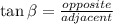
$\tan \beta=(opposite)/(adjacent)$

In this case:

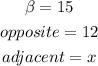
$\begin{gathered} \beta=15\degree \\ opposite=12 \\ adjacent=x \end{gathered}$

Therefore, substituting values and solving for "x", you get:

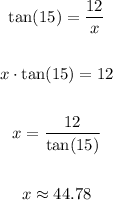
$\begin{gathered} \tan (15\degree)=(12)/(x) \\ \\ x\cdot\tan (15\degree)=12 \\ \\ x=(12)/(\tan (15\degree)) \\ \\ x\approx44.78 \end{gathered}$

Hence, the answer is: Option D.

Please log in or register to add a comment.