We can draw the following picture to give us an idea of what we are given
We notice that the point (3,-5) is on the down side of y=-1. Since we want to reflect this point over y=-1, it means that we want to find a point (x,y) that is on the up side of y=-1 that is as the same distance from y=-1 as the point (3,-5). To find this point, we draw first a vertical line that passes through the point (3,-5). Then, we "walk" along this line until we cross the line y=-1, so we can calculate the distance from (3,-5) to y=-1. Once we find this distance, we keep walking until we walk the desired distance. A picture of this would look like this
From this picture, we know that the desired point lays on the vertical line that passes through (3,-5). This means that the should have the same x -coordinate (namely 3). We also notice that the distance from (3,-5) to the line y=-1 is 4. So the distance from the line to the desired point should also be 4. We can see that we can calculate the distance from (3,-5) to the line y=-1 by simply subtracting -1 and -5. That is (1-(-5))=5-1 = 4.
Let h be the y coordinate of the desired point, since the distance should also be 4, we must have
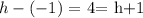
Finally, we can subtract 1 on both sides, so we get
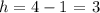
So the desired point is (3,3), which is the result of reflecting the point (3,-5) over y=-1