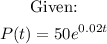
A) What will be the rate of change of the population in 10 years.
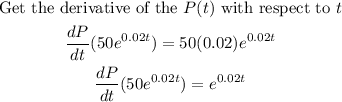
Substitute t = 10, to the derivative of P(t)
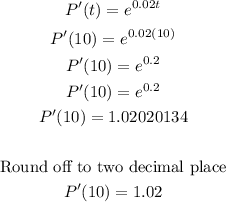
Therefore, the rate of change of the population in 10 years is 1.02 million.
B) What will be the relative rate of the population in t years? Is this rate constant?

The rate is not constant, as it depends on how much time t has passed.