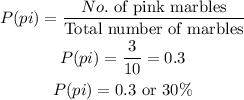Question

A marble is drawn randomly from a jar that contains 5 purple marbles, 2 blue balls, and 3 pink marbles. Find the probability of randomly selecting

Answer 1

Let's begin by identifying key information given to us:

Jar contains: 5 purple marbles, 2 blue balls, and 3 pink marbles

Total number of marbles = 5 + 2 + 3 = 10 marbles

Purple marbles = 5, Blue marbles = 2, Pink marbles = 3

`P=\frac{No.\text{ of specific marbles colour}}{\text{Total number of marbles}}`

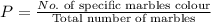
Probability of selecting randomly without replacement:

a) Purple marble

`\begin{gathered} P(P)=\frac{No.\text{ of purple marbles}}{\text{Total number of marbles}} \\ P(P)=(5)/(10)=0.5 \\ P(P)=0.5\text{ or 50\%} \end{gathered}`

b) Blue marble

`\begin{gathered} P(B)=\frac{No.\text{ of blue marbles}}{\text{Total number of marbles}} \\ P(B)=(2)/(10)=0.2 \\ P(BP)=0.2\text{ or 20\%} \end{gathered}`

c) Pink marble

`\begin{gathered} P(pi)=\frac{No.\text{ of pink marbles}}{\text{Total number of marbles}} \\ P(pi)=(3)/(10)=0.3 \\ P(pi)=0.3\text{ or 30\%} \end{gathered}`