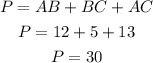ANSWER
P = 30
Step-by-step explanation
The perimeter of a triangle is the sum of the length of its sides.
This triangle is:
To find its perimeter we have to find the side lengths, that are the distance between each pair of points.
The length of side AB is:
![\begin{gathered} AB=\sqrt[]{(4-(-8))^2+(-1-(-1))^2} \\ AB=\sqrt[]{(4+8)^2+0} \\ AB=\sqrt[]{12^2} \\ AB=12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jkmr5vmfu7qublnsj02xxnhdrhy4xlgo44.png)
The length of side BC is:
![\begin{gathered} BC=\sqrt[]{(4-4)^2+(-1-4)^2} \\ BC=\sqrt[]{0+5^2} \\ BC=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6vg4s51ah54pkw1yetn3ay6o8gu81oi4pl.png)
Finally, side AC is:
![\begin{gathered} AC=\sqrt[]{(-8-4)^2+(-1-4)^2} \\ AC=\sqrt[]{12^2+5^2} \\ AC=\sqrt[]{144+25} \\ AC=\sqrt[]{169} \\ AC=13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1d4gmgfvx4fu9qd3lf0vsreqetmt9w93vv.png)
Finally, the perimeter of the triangle is: