Given,
The frequency of the source, f=1216 Hz
The speed with which the car is moving away from the source, v₀=28 m/s
The speed of the sound, v=343 m/s
The frequency with which the observer hears the sound is given by,

On substituting the known values,
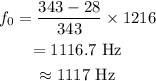
Thus the frequency heard by the observer is 1117 Hz. Therefore the correct answer is option 4.