Question

A slide 4.1 meters long makes an angle of 35 degrees with the ground. To the nearest tenth of a meter, how far above the ground is the top of the slide? (image attached)

Answer 1

2.4 meters

Explanation:

In the given right triangle:

• The side length ,opposite ,35° = x

,

• The length of the ,hypotenuse ,= 4.1 meters

We want to solve for x.

Using the trigonometric ratios of right triangles:

`\begin{gathered} \sin\theta=(Opposite)/(Hypotenuse) \\ \implies\sin35\degree=(x)/(4.1) \end{gathered}`

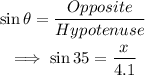
Cross multiply:

`\begin{gathered} x=4.1*\sin35\degree \\ x=2.35 \\ x\approx2.4\text{ meters} \end{gathered}`

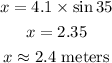
The top of the slide is approximately 2.4 meters above the ground.