Part A.
The speed is given by
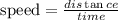
In our case, the distance is 3.8x10^5 kilometers and the time is 2.16x10^3 minutes. By substituting these values we get
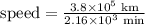
Part B.
We can rewrite the speed as
![\text{speed}=(\frac{3.8*10^5\operatorname{km}}{1})((1)/(2.16*10^3\min))]()
which is the product of two fractions.
Part C.
The first fraction is
![\frac{3.8*10^5\operatorname{km}}{1}=3.8*10^5\operatorname{km}]()
and the second fraction is
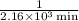
This fraction can be written as
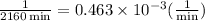
Therefore, the answers for part C are
![\begin{gathered} \text{first fraction: }3.8*10^5\operatorname{km} \\ \text{second fraction: }0.463*10^(-3)((1)/(\min)) \end{gathered}]()
Part D.
Yes, the values are written in scientific notation. Then, the speed is given by
![\text{speed}=(3.8*10^5\operatorname{km})(\text{ }0.463*10^(-3)(1)/(\min))]()
which gives
![\text{speed}=(3.8*0.463*10^(5-3))(\frac{\operatorname{km}}{\min }]()
then, the result is
![\text{speed}=1.76*10^2\frac{\operatorname{km}}{\min }]()