Question

Polygon ABCD with A (0,4), B (-4, 8), C (3, 3), and D (4, -2), is dilated by a scale factor of /2. What are the new coordinates? Is this a reduction or enlargement? *

Answer 1

The formula for dilations with center at origin is

`\begin{gathered} D_(O,k)(x,y)=(kx,ky) \\ \text{ Where O is the center of dilation at (0,0) and} \\ k\text{ is the scale factor} \end{gathered}`

Likewise when

*k > 1, the dilation is an enlargement

*k < 1, the dilation is a reduction

*k = 1, the dilation is a congruence

So, in this case, you have

`k=(1)/(2)<1`

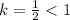
Then, the dilation of the polygon is a reduction.

Now, finding the new coordinates of the polygon, you have

`\begin{gathered} A(0,4)\rightarrow A^(\prime)((1)/(2)\cdot0,(1)/(2)\cdot4)=A^(\prime)(0,2) \\ \end{gathered}`
`B(-4,8)\rightarrow B^(\prime)((1)/(2)\cdot-4,(1)/(2)\cdot8)=B^(\prime)(-2,4)`

`C(3,3)\rightarrow C^(\prime)((1)/(2)\cdot3,(1)/(2)\cdot3)=C^(\prime)(1.5,1.5)`

`D(4,-2)\rightarrow D^(\prime)((1)/(2)\cdot4,(1)/(2)\cdot-2)=D^(\prime)(2,-1)`

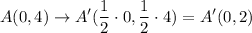
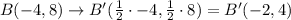
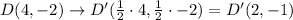
Therefore, the correct answer is C. A'(0,2), B'(-2,4), C'(1.5,1.5), D'(2,-1): Reduction.