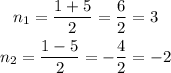Question

A number n is 6 less than the square of n. how many possible values are there for n

Answer 1

We can write the question as a a polynomial as it follows:

`n=n^2-6`

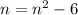
The values that makethis expression true are the zero of the following polynomial:

`f(n)=n^2-n-6`

We can use Bhaskara to find the values:

`n_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where:

`\begin{gathered} a=1 \\ b=-1 \\ c=-6 \end{gathered}`

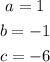
Substituting the values, we find:

`n_(1,2)=\frac{1\pm\sqrt[]{1-4(1)(-6)}}{2}=\frac{1\pm\sqrt[]{25}}{2}=(1\pm5)/(2)`

Before solving, we can see that there will realy have two real numbers for n. So the answer is the third optio: Two.

We can go ahead and find the values:

`\begin{gathered} n_1=(1+5)/(2)=(6)/(2)=3 \\ n_2=(1-5)/(2)=-(4)/(2)=-2 \end{gathered}`