Given,
The height of the building upto 9th floor is 39 meters.
The angle of elevation is 31 degree.
The angle of depression is 42 degree.
The diagram of the building and taller building is,
Consider,
AB is the height of the building upto 9th floor.
CE is the height of the taller biulding.
BE=AD is the distance between building and taller building.
Taking triangle ADE,
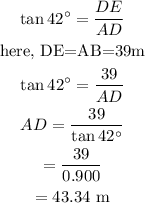
The distance between the building and the taller building is 43.34 m (approximately).
Taking triangle ADC,
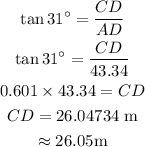
The height of the taller building is,

The height of the taller building is 65.1 meter.