1 Answer

Babay · Answer 1 · 2023-09-19T11:06:41+0000

Answer:

$\begin{gathered} CP=√(11) \\ m\operatorname{\angle}C=56.44 \end{gathered}$

Step-by-step explanation:

Step 1. The information that we have is that

• PQ=5

,

• CQ=6,

and that PQ is tangent to circle C.

Since PQ is a tangent line, it forms a 90° angle with the circumference, and the triangle is a right triangle.

We need to find CP and the measure of angle C (m

Step 2. To find CP we use the Pythagorean theorem:

In this case:

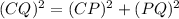
Substituting the known values:

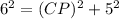
Solving for CP:

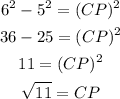
$\begin{gathered} 6^2-5^2=(CP)^2 \\ 36-25=(CP)^2 \\ 11=(CP)^2 \\ √(11)=CP \end{gathered}$

The value of CP is:

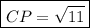
$\boxed{CP=√(11)}$

Step 3. To find the measure of angle C, we use the trigonometric function sine:

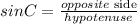
$sinC=\frac{opposite\text{ side}}{hypotenuse}$

The opposite side to angle C is 5 and the hypotenuse is 6:

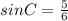
Solving for C:

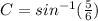
Solving the operations:

$\begin{gathered} C=s\imaginaryI n^(-1)(0.83333) \\ C=56.44 \\ \downarrow \\ \boxed{m\operatorname{\angle}C=56.44} \end{gathered}$

Answer:

$\begin{gathered} CP=√(11) \\ m\operatorname{\angle}C=56.44 \end{gathered}$

Please log in or register to add a comment.