Remember that 1 foot is equal to 12 inches.
a)
To find the length in feet only, convert 6 inches to feet and add that amount to the length of 12 feet:
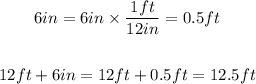
Then, the length of the swimming pool in feet is 12.50.
b)
To find the width in feet only, convert 4 inches to feet and and that amount to the width of 30 feet:
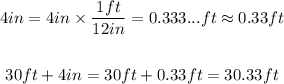
Then, the wudth of the swimming pool in feet (to the nearest hundredth) is 30.33.
c)
Draw a diagram of the pool with the sidewalk to visualize the situation:
The width and the length of the larger rectangle that includes the sidewalk are 4ft larger than the dimensions of the swimming pool because the sidewalk is 2ft wide.
To find the area of the sidewalk, subtract the area of the smaller rectangle from the area of the larger rectangle:
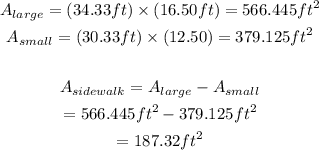
Then, the area of the sidewalk is 187.32 square feet.