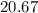Step-by-step explanation
In the first case, we will find the area of the triangle. This is given as;
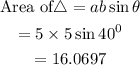
To get the area of the semicircle we will require the diameter of the semicircle, which is the unknown side of the triangle.
Let the unknown side be x
Therefore, we can use the cosine rule.
![\begin{gathered} x=\sqrt[]{a^2+b^2-2ab\cos \theta} \\ x=\sqrt[]{5^2+5^2-2*5*5\cos 40^0} \\ x=\sqrt[]{25^{}+25^{}-50\cos 40^0} \\ x=\sqrt[]{50^{}-50\cos 40^0} \\ x=3.4202 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1f35aj2j1uid3trpuuxsfiexc0osqk9e9a.png)
x represents the diameter of the semicircle. We can then have the radius as half of x.
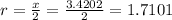
The area of the semicircle is given as
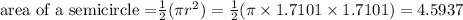
Therefore, the area of the shape is the sum of the triangle and the semi-circle.
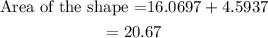
Answer: