Given: A function-
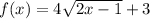
Required: To determine the point where the function starts.
Explanation: To determine where the function starts, we need to determine the domain and range of the function. The domain of a function is the set of x values for which the function is defined.
The square root is not defined for negative values. Hence the domain of the function is the set of all x values greater than or equal to zero as follows-
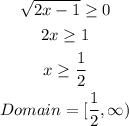
And the range for a function of the type-
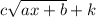
is-
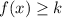
Hence, the range of the function is-
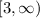
Hence, the function starts at the point (1/2,3).
Final Answer: Option D is correct.