Question

In a survey of 200 people, 32% had a son, 30% had a daughter, and 11% had both a sonand a daughter. What is the conditional probability that a person who has a son also hasa daughter? Round to the nearest whole number.

Answer 1

We have the following probabilites:

`\begin{gathered} P(\text{had a son)=P(s)}=0.32 \\ P(\text{had a daughter)}=P(d)=0.3 \\ P(\text{had both son and daughter)}=P(d\cap s)=0.11 \end{gathered}`

Following the definition of conditional probability:

`P(A|B)=(P(A\cap B))/(P(A))`

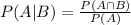
In this case, we want to calculate the conditional probability that a person has a daughter given that he/she already has a son. Then, the probability is:

`P(d|s)=(P(d\cap s))/(P(s)))=(0.11)/(0.32)=0.34`

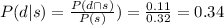
therefore, the conditional probability that a person who has a son also has a daughter is 34%