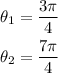First, add 1 to both members of the equation:
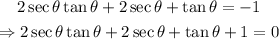
Next, factor out 2secθ from the first two terms, and group the third and fourth therms:
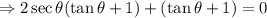
Factor out (tanθ+1):
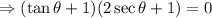
Since the product of two factors is equal to 0, then, the equation is true whenever each of them is equal to 0 separately. This leads to two cases:
Case 1: tanθ+1=0
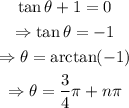
For n=0 and n=1, we get solutions on the interval [0,2π)
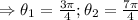
Case 2: 2secθ+1=0
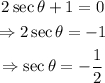
Since the absolute value of the secant function is always greater or equal to 1, there are no real solutions for this case.
Therefore, all the solutions to the equation in the interval [0,2π) are: