Given a cone and a scoop of ice cream.
To determine: The cubic centimeters of ice cream
Solution:
The ice is a combination of the shape of a cone and a hemisphere. To find the cubic centimeters of the ice cream, we would find the volume of the cone and the hemisphere.
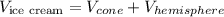
![\begin{gathered} V_{\text{cone}}=(1)/(3)\pi r^2h \\ d=6\operatorname{cm}(given) \\ r=(d)/(2)=\frac{6\operatorname{cm}}{2}=3\operatorname{cm} \\ h=13\operatorname{cm}(\text{given)} \end{gathered}]()
![\begin{gathered} V_{\text{cone}}=(1)/(3)\pi r^2h \\ V_{\text{cone}}=(1)/(3)\pi*3^2*13 \\ V_{\text{cone}}=39\pi\operatorname{cm}^3 \end{gathered}]()
![\begin{gathered} V_{\text{hemisphere}}=(2)/(3)\pi r^3 \\ r=3\operatorname{cm} \\ V_{\text{hemisphere}}=(2)/(3)\pi*3^3 \\ V_{\text{hemisphere}}=18\pi cm^3 \end{gathered}]()
![\begin{gathered} V_{\text{ice cream}}=V_(cone)+V_(hemisphere) \\ V_{\text{ice cream}}=39\pi cm^3+18\pi cm^3 \\ V_{\text{ice cream}}=57\pi cm^3 \\ V_{\text{ice cream}}=179.07\operatorname{cm}^3 \end{gathered}]()
Hence, the number of cubic centimeters of ice cream is 179.07cm³