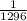Question

. The faces of a fair cube are numbered1 through 6; the probability of rolling anynumber from 1 through 6 is equally likely. Ifthe cube is rolled 4 times, what is the probabilitythat the number 6 will appear on the top face all4 times?

Answer 1

The probability of an event is expressed as

`Pr(\text{event)}=\frac{\text{Number of desired outcome}}{Number\text{ of possible outcome}}`

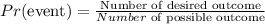
Given a fair cube which has its faces numbered 1 to 6 as [1,2,3,4,5,6].

This implies that the number of possible outcome equals 6.

Given that a 6 will appear when rolled, the probability is thus

`\begin{gathered} Pr(6)=\frac{\text{Number of }6\text{ in the far cube}}{Number\text{ of possible outcome}}\text{ } \\ =(1)/(6) \\ \end{gathered}`

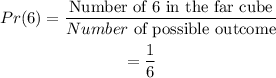
When the cube is rolled four times, the probability thus becomes

`\begin{gathered} Pr(^{_{}}6)=(1)/(6)*(1)/(6)*(1)/(6)*(1)/(6) \\ \Rightarrow Pr(^{_{}}6\text{ four times)=}(1)/(1296) \end{gathered}`

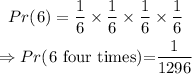
Hence, the probability that the number 6 will appear four times is

`(1)/(1296)`