Question

The Euler buckling load of a column with square cross-section (side length 5 cm) will be _____ times the Euler buckling load of an equivalent column with circular cross-section (diameter 5 cm).

Answer 1

The formula for Euler's buckling load, is:

`P=(\pi^2EI)/(L^2)`

Where E is the Young's modulus of the material, I is the cross-sectional area moment of inertia of the column, and L is the length of the column.

If we keep the length and the Young's modulus constant, the ratio between the buckling load of two columns with different cross-sectional area moment of inertia (a square and a circle) will be:

`(P_s)/(P_c)=(((\pi^2EI_s)/(L^2)))/(((\pi^2EI_c)/(L^2)))=(I_s)/(I_c)`

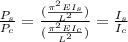
Where the subindex s refers to the square and the subindex c refers to the circle.

The area moment of inertia of a square with side S is given by:

`I_s=(S^4)/(12)`

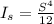
The area moment of inertia of a circle with diameter S is given by:

`I_c=\pi\cdot(S^4)/(64)`

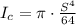
Notice that in this case, the side length of the square is the same as the diameter of the circle. Then:

`(I_s)/(I_c)=(((S^4)/(12)))/(((\pi S^4)/(64)))=(64S^4)/(12\pi S^4)=(64)/(12\pi)=(16)/(3\pi)\approx1.7`

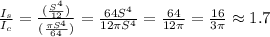
Then:

`\begin{gathered} (P_s)/(P_c)\approx1.7 \\ \Rightarrow P_s\approx1.7P_c \end{gathered}`

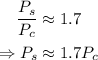
Therefore, the Euler's buckling load of a column with square cross-section with side length 5cm will be 16/(3π) times the Euler buckling load of an equivalent column with circular cross-section and diameter 5cm.

Approximately, the Euler buckling load of a column with square cross-section will be 1.7 times that of a column with circular cross section.