Solution.
Calculate the standard deviation
The formula is given below
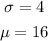
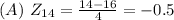
P(x>-0.5) = 0.69146
In percentage, P(x>Z) = 69.15% (2 decimal places)
THE PERCENT OF CUSTOMERS WHO WAIT FOR AT LEAST 14 MINUTES
BEFORE BEING SEATED is 69.15%
(B)
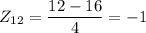
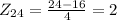
![\begin{gathered} P\left(-1Thus, THE PERCENT OF CUSTOMERS WHO WAIT BETWEEN 12 AND 24 MINUTES BEFORE BEING SEATED is 81.86%<p></p><p>(C)</p>[tex]Z_(21)=(21-16)/(4)=1.25]()
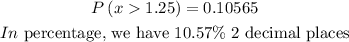
Thus, THE PERCENT OF CUSTOMERS WHO WAIT AT LEAST 21 MINUTES BEFORE BEING SEATED is 10.57%