Given:
Ratio of corresponding sides = 10 : 7
Perimeter of smaller table = 42
Total ratio = 10 + 7 = 17
Let's find the perimeter of the larger table.
Given that both tables are similar, it means the corresponding sides are proportional.
To find the ratio of the larger table, let's first find the total perimeter of the both tables:
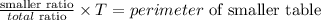
Where T represents the total ratio.
Thus, we have:
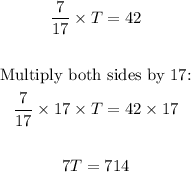
Divide both sides by 7:
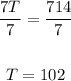
The total perimeter is 102.
To find the permeter of the larger table, we have:
Perimeter of larger table = Total perimeter - perimeter of smaller table.
Perimeter of larger table = 102 - 42
Perimeter of larger table = 60
Therefore, the perimeter of the larger table is 60.
ANSWER:
60