Question

n sync On average, a person's heart beats about 4.2 x 10^7 times per year. There are about 7,600,000,000 people in the world. Use this data to approximate the number of heartbeats for all the people in the world per year. Expressing your answer in scientific notation in the form a x 10^b what are the values of a and b?

Answer 1

First, notice that if there are 4.2*10^7 hearbeats per year per person and there are 7,600,000,000 people in the world, then the total number of heartbeats in the world per year is equal to:

`(4.2\cdot10^7)(7,600,000,000)`

Rewrite the number 7,600,000,000 using scientific notation. Moving the decimal point 9 places to the left:

`7,600,000,000=7.6\cdot10^9`

Therefore, the number of heartbeats per year can be expressed as:

`(4.2\cdot10^7)\cdot(7.6\cdot10^9)`

Use the commutative property of multiplication to rewrite the product:

`4.2\cdot7.6\cdot10^7\cdot10^9`

Multiply 4.2 times 7.6:

`31.92\cdot10^7\cdot10^9`

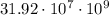
Use the properties of the exponents to rewrite (10^7)(10^9):

`31.92\cdot10^(7+9)=31.92\cdot10^(16)`

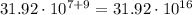
Move the decimal point one place to the left by increasing by 1 the exponent of the power of 10:

`3.192\cdot10^(17)`

Comparing this number with the expression a x 10^b:

`\begin{gathered} a=3.192 \\ b=17 \end{gathered}`

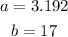
Therefore, there is a total of 3.192 x 10^17 human heartbeats per year.