Given the function
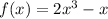
Using the graphical method,
The graph of the given function is shown below
From the graph of the function,
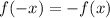
Hence, the given function is Odd
Alternatively
Replacing x with -x and solving
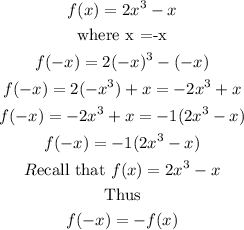
It can be seen from the above deduction that
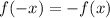
Hence, the function f(x)=2x³-x is odd