Question

Suppose Aldo places $2000 in an account that pays 16% interest compounded each year.Assume that no withdrawals are made from the account.Follow the instructions below. Do not do any rounding.(a) Find the amount in the account at the end of 1 year.$(b) Find the amount in the account at the end of 2 years.$

Answer 1

It is given that $2000 was placed in an account that pays 16% interest compounded each year.

The Compound Interest Formula is given as:

`A=P(1+(r)/(n))^(nt)`

Where P is the amount placed in the account, r is the interest rate, n is the number of times the interest is compounded in a year, and t is the time passed in years.

(a) It is required to find the amount after 1 year.

Substitute P=2000, r=16%=0.16, n=1, and t=1 into the equation:

`\begin{gathered} A=2000(1+(0.16)/(1))^(1(1)) \\ \Rightarrow A=2000(1+0.16)^1=2000(1.16)=\$2320 \end{gathered}`

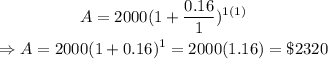
(b) It is required to find the amount after 2 years.

Substitute P=2000, r=16%=0.16, n=1, and t=2 into the equation:

`\begin{gathered} A=2000(1+(0.16)/(1))^(1(2)) \\ \Rightarrow A=2000(1+0.16)^2=2000(1.16)^2=2000(1.3456)=\$2691.2 \end{gathered}`

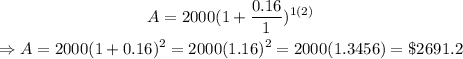
Answers:

(a) $2320

(b) $2691.2