Question

The bus comes to a stop near your house every morning at a random time between 6:45 and 6:50. You arrive at the bus stop at a random time between 6;40 and 6:45 every morning and wait until the bus comes. What is the probability that you will wait less than 4 minutes for the bus to arrive?

Answer 1

What we have here is an example of a geometric probability.

This is the probability that an event will occur within the given area of a figure. That is the ratio of the desired area (required outcomes) to the total area (all possible outcomes).

We shall sketch a graph for the sake of simplicity, as follows;

What we now have is a graph showing the arrival,time of the bus on the vertical axis and, your own arrival time on the horizontal axis.

Next we would shade the area which indicates your waiting time.

Note that the experiment ia aimed at a waiting time of less than 4 minutes.

Therefore, if you arrived at 6:40, a less than 4 minutes waiting time would be between 6:41 and 6:45 (and nothing beyond that).

The area of the shaded region shall be;

`\begin{gathered} \text{Area of triangle}=(1)/(2)b* h \\ b=4\text{ units} \\ h=4\text{ units} \\ \text{Area}=(1)/(2)*4*4 \\ \text{Area}=(1)/(2)*16 \\ \text{Area}=8\text{ units} \end{gathered}`

The area of the entire region both shaded and unshaded (all posible outcomes) shall be:

`\begin{gathered} \text{Area of a square}=l* w \\ l=5\text{ units} \\ w=5\text{ units} \\ \text{Area}=5*5 \\ \text{Area}=25units^2 \end{gathered}`

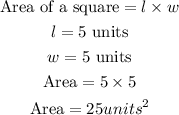
ANSWER:

The probability that you will wait less than 4 minutes for the bu to arrive is;

`\begin{gathered} P\lbrack E\rbrack=\frac{\text{area of shaded region}}{area\text{ of entire region}} \\ P\lbrack E\rbrack=(8)/(25) \end{gathered}`

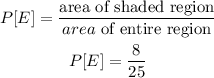
The probability is 8/25

OR

The probability is 0.32 (expressed as a decimal)