Question

Look at the cordinates below and write a linear equation (3,4) and (8,3)

Answer 1

Hello!

A linear equation has the form y = ax +b.

We also can call it the slope-intercept form.

We have two points, that I will name 1 and 2:

• (x1, y1) = (3, 4)

,

• (x2, y2) = (8, 3)

The first step is to find the slope (variable a). We must use the formula below:

`Slope=(y_2-y_1)/(x_2-x_1)`

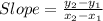
So, let's replace it with the values that we know:

`Slope=(3-4)/(8-3)=-(1)/(5)`

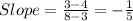
Now we know variable a, we must find the variable b too. So, we can replace x and y in the equation with the coordinates of the point (x1, y1). Look:

`\begin{gathered} y=ax+b \\ 4=-(1)/(5)\cdot3+b \\ 4=-(3)/(5)+b \\ 4+(3)/(5)=b \\ b=(23)/(5) \end{gathered}`

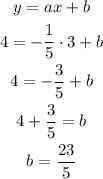
So, the equation will be:

`\begin{gathered} y=ax+b \\ y=-(1)/(5)x+(23)/(5) \end{gathered}`

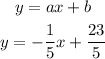
Look at the graph of this equation below: