Question

A town’s population increases at a constant rate. In 2010 the population was 54,000. By 2012 the population had increased to 79,000. If this trend continues, predict the population in 2016. The population will be ____ in 2016.

Answer 1

Given:

A town’s population increases at a constant rate.

In 2010: population = 54,000

In 2012: population = 79,000

The will use the function of the exponential growth:

`P(t)=P_0\cdot(1+r)^t`

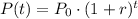
where: P₀ is the initial population

r is the rate of increase

t is the number of years from 2010

So, we'll substitute with the given values to find the rate of increase

`\begin{gathered} P_0=54000 \\ P=79000 \\ t=2012-2010=2 \\ \\ 79000=54000\cdot(1+r)^2 \end{gathered}`

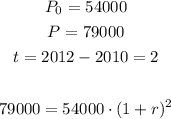
Solve the last equation to find (r) as follows:

`\begin{gathered} (79000)/(54000)=(1+r)^2 \\ \\ (1+r)^2=(79)/(54) \\ \\ 1+r=\sqrt[]{(79)/(54)} \\ \\ r=\sqrt[]{(79)/(54)}-1\approx0.2095 \end{gathered}`

We will use the value of (r) to find the population in 2016

So, t = 2016 - 2010 = 6

`P(6)=54000\cdot(1+0.2095)^6\approx169,081`

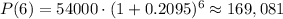
So, the answer will be:

The population will be 169,081 in 2016.