Given:
The first brand is 30% anti-freeze
The second brand is 70% anti-freeze.
We want to make a 60 gallons mixture that has 40% anti-freeze.
Solution
Let the gallons of the first brand be x
Hence the gallons of the second brand would be:
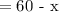
The gallons of the first brand that would be pure anti-freeze:
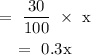
The gallons of the second brand that would be pure anti-freeze:
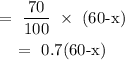
The gallons of the mixture that would be pure anti-freeze:
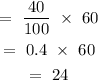
On mixing, we have the equation:
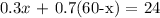
When we solve for x, we have:

Hence, the gallons of the first brand required to obtain a mixture of 40% anti-freeze is 45 gallons.
The gallons of the second brand required would be:
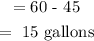
Answer:
First brand = 45 gallons
Second brand = 15 gallons