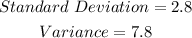The data is given to be:
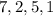
Standard Deviation
The formula used to calculate the standard deviation of a sample data is given to be:
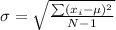
where
σ=population standard deviation
N=the size of the population
xi=each value from the population
μ=the population mean
The sample mean is calculated as shown below:
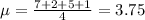
Therefore, we can calculate the standard deviation to be:
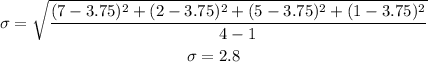
Variance
The variance is the square of the standard deviation. Therefore, we can calculate the variance as follows:
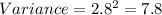
ANSWERS