Question

Find the vertex of each quadratic function by completing the square

Answer 1

We can see that

`(x+2)^2=x^2+4x+4`

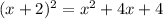
By comparing this expression with our quadratic function, we get

`y\questeq x^2+4x+4-4-16`

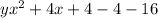
where we added and substracted 4, which gives zero. Now, we can write

`\begin{gathered} y=(x+2)^2-4-16 \\ y=(x+2)^2-20 \end{gathered}`

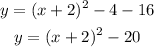
Now, the quadratic function in vertex form is given by

`y=a(x+h)^2+k`

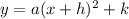
where the point (h,k) is the vertex. By comparing our last result and this expression, we can see that h=2 and k=-20. Then, the vertex is at point (2,-20).