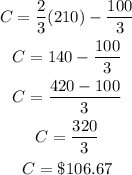Since, the cost C in dollars is a linear function of the length L in feet, we can write:

Where
m is the slope
b is the y-intercept of the line graphed.
The points are in the from (L, C) which is (length, cost). Given:
(80, 20) and (200, 100)
The slope (m) is:

Let the points be:
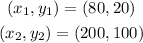
So slope is:
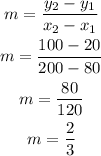
The equation becomes:
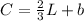
Let's take the point (L, C) = (80, 20) and find out b:
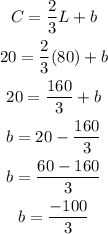
The formula for the function is:
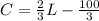
The cost of installing 210 feet of pipe:
We plug in L = 210 into formula and find C: