Question

find the horizontal and vertical asymptots,b) find the continuity intervalc) find discontinuity and type of discontinuity

Answer 1

The function given is,

`f(x)=\frac{1}{\sqrt[]{x+1}}`

The graph of this function:

We can also find the asymptotes the following way:

Horizontal Asymptote

`\begin{gathered} f(x)=\frac{1}{\sqrt[]{x+1}} \\ y=\frac{1}{\sqrt[]{x+1}} \\ y=\frac{(1)/(x)}{\sqrt[]{(x)/(x)+(1)/(x)}} \\ y=\frac{(1)/(x)}{\sqrt[]{1+(1)/(x)}} \\ as \\ x\rightarrow\infty \\ y\rightarrow0 \end{gathered}`

As for Vertical Asymptote,

`\begin{gathered} x+1\\eq0 \\ x\\eq-1 \\ ------- \\ VA\rightarrow x=-1 \end{gathered}`

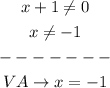
(a)

From the graph, we can see that horizontal asymptote is at y = 0

And, the vertical asymptote is at x = -1

The graph below (with asymptotes showing):

(b)

As seen from the graph, the function is continuous from x > -1

There aren't any function at x = -1 and less

So, the continuity interval is

`x>-1`

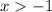
(c)

The function is discontinuous at x = -1

This is an infinite discontinuity because it's a vertical asymptote.